September 29, 2010
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 | \documentclass[12pt]{article}\usepackage[papersize={6in, 9.1in}, text={5.5in, 8.8in}]{geometry}\usepackage{amsmath}\usepackage{mathspec}\usepackage{fontspec}\defaultfontfeatures{Scale=MatchLowercase}\setmainfont[Mapping=tex-text]{Minion Pro}%\setmainfont[Mapping=tex-text]{Hoefler Text}%\setmainfont[Mapping=tex-text]{Garamond}\setsansfont[Mapping=tex-text]{Candara}%\setsansfont[Mapping=tex-text]{Myriad Pro}%\setsansfont[Mapping=tex-text]{Comic Sans MS}%\setmonofont{Courier}\setmonofont{Monaco}\usepackage{paralist}\newcommand{\fpd}[2]{\ensuremath{\frac{\partial{#1}}{\partial{#2}}}}\begin{document}\thispagestyle{empty}The Cauchy distribution is a symmetric distribution on$(-\infty,\infty)$ with pdf\begin{equation*} f_X(x;\theta,\gamma) = \frac1\pi \cdot \frac{\gamma}{(x-\theta)^2+\gamma^2}\end{equation*}In this paper, we only deal with the case $\theta=0$.Consider two independent Gaussian random variables $X,Y\sim N(0,1)$.We will prove that the ratio $X/Y$ is a Cauchy distribution by\begin{inparaenum}[(1)]\item defining the transformation $U=X/Y$ and $V=|Y|$,\item finding the joint pdf $F_{U,V}(u,v)$, and\item integrating out $V$ to obtain the marginal pdf of $U$.\end{inparaenum}Unfortunately, the mapping $U=X/Y$ and $V=|Y|$ is not one-to-one:the two points $(x,y)$ and $(-x,-y)$ map to the same $(u,v)$We need to partition $(X,Y)$ into $A_0,A_1,A_2$ such that the mappingfrom $A_i$ to $(U,V)$ is one-to-one.\begin{enumerate} \item $A_0=\{(X,Y):Y=0\}$: This exceptional case does not happen because $\Pr[Y=0]=0$ when $Y\sim N(0,1)$. \item $A_1=\{(X,Y):Y>0\}$: The mapping $U=X/Y$, $V=|Y|$ is one-to-one, and the inverse mappings are $h_{11}(u,v)=uv$, $h_{21}=v$. \item $A_2=\{(X,Y):Y<0\}$: The mapping $U=X/Y$, $V=|Y|$ is one-to-one, and the inverse mappings are $h_{12}(u,v)=-uv$, $h_{22}=-v$.\end{enumerate}\begin{equation*}\begin{array}{lllll} J_1 & = \begin{vmatrix} \fpd{h_{11}}{u} & \fpd{h_{11}}{v} \\ \fpd{h_{21}}{u} & \fpd{h_{21}}{v} \end{vmatrix} & = \begin{vmatrix} \fpd{uv}{u} & \fpd{uv}{v} \\ \fpd{v}{u} & \fpd{v}{v} \end{vmatrix} &= \begin{vmatrix} v & u \\ 0 & 1 \end{vmatrix} &= v \\ J_2 &= \begin{vmatrix} \fpd{h_{12}}{u} & \fpd{h_{12}}{v} \\ \fpd{h_{22}}{u} & \fpd{h_{22}}{v} \end{vmatrix} &= \begin{vmatrix} \fpd{(-uv)}{u} & \fpd{(-uv)}{v} \\ \fpd{(-v)}{u} & \fpd{(-v)}{v} \end{vmatrix} &= \begin{vmatrix} -v & -u \\ 0 & -1 \end{vmatrix} &= v\end{array}\end{equation*}%%%\begin{equation*} f_{X,Y}(x,y) = \frac{1}{\sqrt{2\pi}}\exp(-x^2/2) \frac{1}{\sqrt{2\pi}}\exp(-y^2/2) = \frac{1}{2\pi}\exp\left(-\frac{x^2+y^2}{2}\right)\end{equation*}%%%\begin{align*} f_{UV}(u,v) &= f_{XY}(h_{11}(u,v),h_{21}(u,v))|J_1| + f_{XY}(h_{12}(u,v),h_{22}(u,v))|J_2| \\ &= \frac{1}{2\pi}\exp\left(-\frac{(uv)^2 + v^2}{2}\right)|v| + \frac{1}{2\pi}\exp\left(-\frac{(-uv)^2 + (-v)^2}{2}\right)|v| \\ &= \frac{v}{\pi}\exp\left(-\frac{v^2(u^2+1)}{2}\right), \qquad -\infty < u < \infty, \quad0<v<\infty \\\end{align*}%%%\begin{alignat*}{2} f_U(u) &= \int_0^\infty \frac{v}{\pi}\exp\left(-\frac{v^2(u^2+1)}{2}\right) dv & \text{integrating out $V$}\\ &= \int_0^\infty \frac{1}{2\pi}\exp\left(-\frac{u^2+1}{2}z\right) dz & \qquad\text{Let $z=v^2$ and $dz=2vdv$} \\ &= \frac{1}{2\pi}\cdot \frac{2}{u^2+1} & \int_0^\infty \exp(-\alpha z) dz = \frac1\alpha \\ &= \frac{1}{\pi}\cdot\frac{1}{u^2+1},\qquad -\infty< u<\infty\end{alignat*}\end{document} |
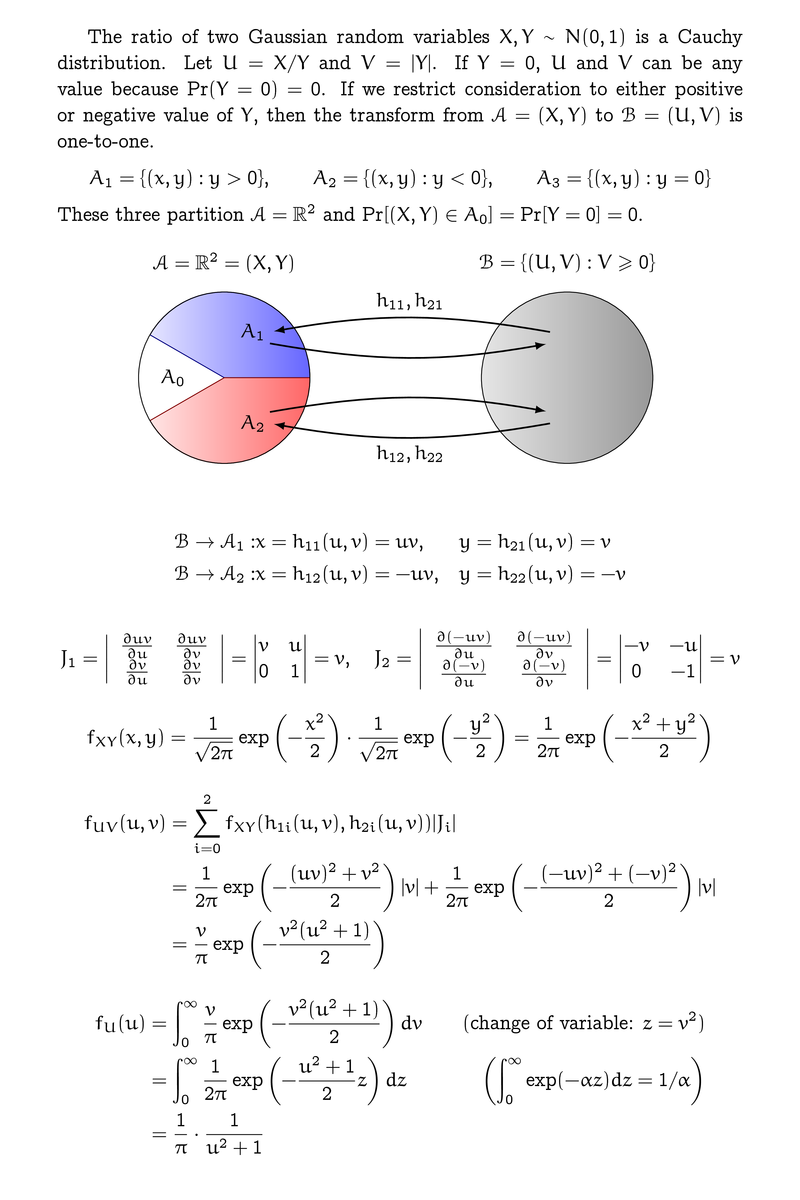
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 | \documentclass[10pt]{article}\pagestyle{empty}\usepackage{amsmath,amssymb,amsthm}\usepackage[papersize={140mm, 210mm}, text={120mm, 200mm}]{geometry}% For fancy fonts\usepackage[T1]{fontenc}\usepackage{ccfonts,eulervm}\usepackage{tikz}\newcommand{\fpd}[2]{\ensuremath{\frac{\partial{#1}}{\partial{#2}}}}\thispagestyle{empty}\begin{document}The ratio of two Gaussian random variables $X,Y\sim N(0,1)$ is aCauchy distribution.Let $U=X/Y$ and $V=|Y|$. If $Y=0$, $U$ and $V$ can be any valuebecause $\Pr(Y=0)=0$.If we restrict consideration to either positive or negative value of$Y$, then the transform from $\mathcal{A}=(X,Y)$ to$\mathcal{B}=(U,V)$ is one-to-one.\begin{equation*} A_1 = \{(x,y): y > 0 \},\qquad A_2 = \{(x,y): y < 0 \},\qquad A_3 = \{(x,y): y = 0 \}\end{equation*}These three partition $\mathcal{A}=\mathbb{R}^2$ and$\Pr[(X,Y)\in A_0]=\Pr[Y=0]=0$.\begin{figure}[h] \centering \begin{tikzpicture} [line/.style ={draw, thick, -latex, shorten >=2pt},] \def\myradius{1.5cm} % left circle \shadedraw[left color=blue!10, right color=blue!60, draw=blue!50!black] (0, 0) -- (\myradius, 0mm) arc (0:150:\myradius) -- cycle; \shadedraw[left color=red!10, right color=red!60, draw=red!50!black] (0, 0) -- (\myradius, 0mm) arc (0:-150:\myradius) -- cycle; \draw (0,0) circle (\myradius); \node at (5mm, 8mm) {$A_1$}; \node at (5mm, -8mm) {$A_2$}; \node at (-9mm, 0mm) {$A_0$}; \node at (0cm, \myradius+5mm) {$\mathcal{A}=\mathbb{R}^2=(X,Y)$}; % right circle \shade[left color=black!10, right color=black!40, draw=black!50!black] (6cm, 0) circle (\myradius); \node at (\myradius*4, \myradius+5mm) {$\mathcal{B}=\{(U,V):V\geq 0\}$}; % arrows \path (\myradius*4-3mm, 8mm) edge [line, bend angle=10, bend right] node [above, midway] {$h_{11},h_{21}$} (8mm, 8mm); \path (8mm, 6mm) edge [line, bend angle=10, bend right] (\myradius*4-3mm, 6mm); \path (\myradius*4-3mm, -8mm) edge [line, bend angle=10, bend left] node [below, midway] {$h_{12},h_{22}$} (8mm, -8mm); \path (8mm, -6mm) edge [line, bend angle=10, bend left] (\myradius*4-3mm, -6mm); \end{tikzpicture}\end{figure}\begin{alignat*}{3} \mathcal{B} \to \mathcal{A}_1:& x=h_{11}(u,v)=uv, &\quad&y=h_{21}(u,v)=v \\ \mathcal{B} \to \mathcal{A}_2:& x=h_{12}(u,v)=-uv, &\quad&y=h_{22}(u,v)=-v\end{alignat*}\begin{equation*} J_1 = \left| \begin{array}{cc} \fpd{uv}{u} & \fpd{uv}{v} \\ \fpd{v}{u} & \fpd{v}{v} \end{array} \right| = \begin{vmatrix} v & u \\ 0 & 1 \\ \end{vmatrix} = v,\quad J_2 = \left| \begin{array}{cc} \fpd{(-uv)}{u} & \fpd{(-uv)}{v} \\ \fpd{(-v)}{u} & \fpd{(-v)}{v} \end{array} \right| = \begin{vmatrix} -v & -u \\ 0 & -1 \\ \end{vmatrix} = v\end{equation*}\begin{equation*} f_{XY}(x,y) = \frac{1}{\sqrt{2\pi}}\exp\left(-\frac{x^2}{2}\right) \cdot \frac{1}{\sqrt{2\pi}}\exp\left(-\frac{y^2}{2}\right) = \frac{1}{2\pi}\exp\left(-\frac{x^2+y^2}{2}\right)\end{equation*}\begin{align*} f_{UV}(u,v) &= \sum_{i=0}^2 f_{XY}(h_{1i}(u,v),h_{2i}(u,v))|J_i| \\ &= \frac{1}{2\pi}\exp\left(-\frac{(uv)^2 + v^2}{2}\right)|v| + \frac{1}{2\pi}\exp\left(-\frac{(-uv)^2 + (-v)^2}{2}\right)|v| \\ &= \frac{v}{\pi}\exp\left(-\frac{v^2(u^2+1)}{2}\right)\end{align*}\begin{alignat*}{2} f_U(u) &= \int_0^\infty \frac{v}{\pi}\exp\left(-\frac{v^2(u^2+1)}{2}\right) dv &\qquad(\text{change of variable: $z=v^2$}) \\ &= \int_0^\infty \frac{1}{2\pi} \exp\left(-\frac{u^2+1}{2}z\right) dz & \left(\int_0^\infty\exp(-\alpha z) dz = 1/\alpha\right) \\ &=\frac{1}{\pi}\cdot\frac{1}{u^2+1}\end{alignat*}\end{document} |
Comments Off on Cauchy distribution: ratio of two gaussian random variables

no comment until now