Funes el memorioso

pdf

\documentclass[12pt]{article}

\usepackage[papersize={6in, 9.1in}, text={5.5in, 8.8in}]{geometry}
\usepackage{amsmath}

\usepackage{mathspec}
\usepackage{fontspec}
\defaultfontfeatures{Scale=MatchLowercase}
\setmainfont[Mapping=tex-text]{Minion Pro}
%\setmainfont[Mapping=tex-text]{Hoefler Text}
%\setmainfont[Mapping=tex-text]{Garamond}
\setsansfont[Mapping=tex-text]{Candara}
%\setsansfont[Mapping=tex-text]{Myriad Pro}
%\setsansfont[Mapping=tex-text]{Comic Sans MS}
%\setmonofont{Courier}
\setmonofont{Monaco}

\usepackage{paralist}

\newcommand{\fpd}[2]{\ensuremath{\frac{\partial{#1}}{\partial{#2}}}}

\begin{document}
\thispagestyle{empty}
The Cauchy distribution is a symmetric distribution on
$(-\infty,\infty)$ with pdf
\begin{equation*}
  f_X(x;\theta,\gamma) =
  \frac1\pi \cdot \frac{\gamma}{(x-\theta)^2+\gamma^2}
\end{equation*}
In this paper, we only deal with the case $\theta=0$.

Consider two independent Gaussian random variables $X,Y\sim N(0,1)$.
We will prove that the ratio $X/Y$ is a Cauchy distribution by
\begin{inparaenum}[(1)]
\item defining the transformation $U=X/Y$ and $V=|Y|$,
\item finding the joint pdf $F_{U,V}(u,v)$, and
\item integrating out $V$ to obtain the marginal pdf of $U$.
\end{inparaenum}

Unfortunately, the mapping $U=X/Y$ and $V=|Y|$ is not one-to-one:
the two points $(x,y)$ and $(-x,-y)$ map to the same $(u,v)$
We need to partition $(X,Y)$ into $A_0,A_1,A_2$ such that the mapping
from $A_i$ to $(U,V)$ is one-to-one.
\begin{enumerate}
  \item $A_0=\{(X,Y):Y=0\}$: This exceptional case does not happen
    because $\Pr[Y=0]=0$ when $Y\sim N(0,1)$.
  \item $A_1=\{(X,Y):Y>0\}$: The mapping $U=X/Y$, $V=|Y|$ is
    one-to-one, and the inverse mappings are $h_{11}(u,v)=uv$,
    $h_{21}=v$.
  \item $A_2=\{(X,Y):Y<0\}$: The mapping $U=X/Y$, $V=|Y|$ is
    one-to-one, and the inverse mappings are $h_{12}(u,v)=-uv$,
    $h_{22}=-v$.
\end{enumerate}
\begin{equation*}
\begin{array}{lllll}
  J_1 & =
  \begin{vmatrix}
    \fpd{h_{11}}{u} & \fpd{h_{11}}{v} \\
    \fpd{h_{21}}{u} & \fpd{h_{21}}{v}
  \end{vmatrix}
  & = 
  \begin{vmatrix}
    \fpd{uv}{u} & \fpd{uv}{v} \\
    \fpd{v}{u} & \fpd{v}{v}
  \end{vmatrix}
  &=
  \begin{vmatrix}
    v & u \\ 0 & 1
  \end{vmatrix}
  &= v \\
  J_2 &= 
  \begin{vmatrix}
    \fpd{h_{12}}{u} & \fpd{h_{12}}{v} \\
    \fpd{h_{22}}{u} & \fpd{h_{22}}{v}
  \end{vmatrix}
  &= 
  \begin{vmatrix}
    \fpd{(-uv)}{u} & \fpd{(-uv)}{v} \\
    \fpd{(-v)}{u} & \fpd{(-v)}{v}
  \end{vmatrix}
  &=
  \begin{vmatrix}
    -v & -u \\ 0 & -1
  \end{vmatrix}
  &= v
\end{array}
\end{equation*}
%%%
\begin{equation*}
  f_{X,Y}(x,y) =
  \frac{1}{\sqrt{2\pi}}\exp(-x^2/2)
  \frac{1}{\sqrt{2\pi}}\exp(-y^2/2) =
  \frac{1}{2\pi}\exp\left(-\frac{x^2+y^2}{2}\right)
\end{equation*}
%%%
\begin{align*}
  f_{UV}(u,v) &= f_{XY}(h_{11}(u,v),h_{21}(u,v))|J_1|
  + f_{XY}(h_{12}(u,v),h_{22}(u,v))|J_2| \\
  &= \frac{1}{2\pi}\exp\left(-\frac{(uv)^2 + v^2}{2}\right)|v| +
  \frac{1}{2\pi}\exp\left(-\frac{(-uv)^2 + (-v)^2}{2}\right)|v| \\
  &= \frac{v}{\pi}\exp\left(-\frac{v^2(u^2+1)}{2}\right),
  \qquad -\infty < u < \infty, \quad0<v<\infty \\
\end{align*}
%%%
\begin{alignat*}{2}
  f_U(u) &=
  \int_0^\infty \frac{v}{\pi}\exp\left(-\frac{v^2(u^2+1)}{2}\right) dv
  & \text{integrating out $V$}\\
  &= \int_0^\infty \frac{1}{2\pi}\exp\left(-\frac{u^2+1}{2}z\right) dz
  & \qquad\text{Let $z=v^2$ and $dz=2vdv$} \\
  &= \frac{1}{2\pi}\cdot \frac{2}{u^2+1}
  & \int_0^\infty \exp(-\alpha z) dz = \frac1\alpha \\
  &= \frac{1}{\pi}\cdot\frac{1}{u^2+1},\qquad -\infty< u<\infty
\end{alignat*}
\end{document}

cauchy

\documentclass[10pt]{article}
\pagestyle{empty}
\usepackage{amsmath,amssymb,amsthm}
\usepackage[papersize={140mm, 210mm}, text={120mm, 200mm}]{geometry}

% For fancy fonts
\usepackage[T1]{fontenc}
\usepackage{ccfonts,eulervm}

\usepackage{tikz}

\newcommand{\fpd}[2]{\ensuremath{\frac{\partial{#1}}{\partial{#2}}}}

\thispagestyle{empty}

\begin{document}
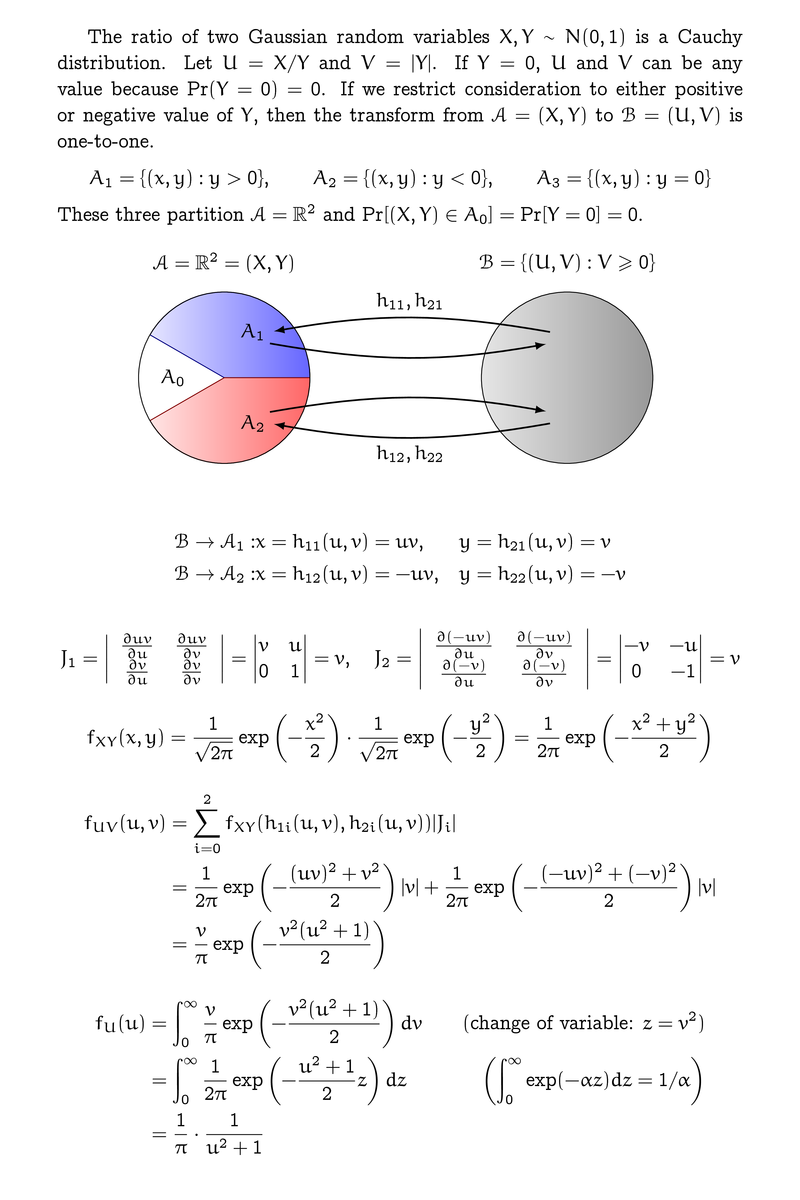
The ratio of two Gaussian random variables $X,Y\sim N(0,1)$ is a
Cauchy distribution.
Let $U=X/Y$ and $V=|Y|$. If $Y=0$, $U$ and $V$ can be any value
because $\Pr(Y=0)=0$.
If we restrict consideration to either positive or negative value of
$Y$, then the transform from $\mathcal{A}=(X,Y)$ to
$\mathcal{B}=(U,V)$ is one-to-one.
\begin{equation*}
  A_1 = \{(x,y): y > 0 \},\qquad
  A_2 = \{(x,y): y < 0 \},\qquad
  A_3 = \{(x,y): y = 0 \}
\end{equation*}
These three partition $\mathcal{A}=\mathbb{R}^2$ and
$\Pr[(X,Y)\in A_0]=\Pr[Y=0]=0$.
\begin{figure}[h]
  \centering
  \begin{tikzpicture}
    [line/.style ={draw, thick, -latex, shorten >=2pt},]
    \def\myradius{1.5cm}
    % left circle
    \shadedraw[left color=blue!10, right color=blue!60,
    draw=blue!50!black]
    (0, 0) -- (\myradius, 0mm) arc (0:150:\myradius) -- cycle; 
    \shadedraw[left color=red!10, right color=red!60,
    draw=red!50!black]
    (0, 0) -- (\myradius, 0mm) arc (0:-150:\myradius) -- cycle;
    \draw (0,0) circle (\myradius);

    \node at (5mm, 8mm) {$A_1$};
    \node at (5mm, -8mm) {$A_2$};
    \node at (-9mm, 0mm) {$A_0$};

    \node at (0cm, \myradius+5mm) {$\mathcal{A}=\mathbb{R}^2=(X,Y)$};

    % right circle
    \shade[left color=black!10, right color=black!40,
    draw=black!50!black] (6cm, 0) circle (\myradius);
    \node at (\myradius*4, \myradius+5mm)
    {$\mathcal{B}=\{(U,V):V\geq 0\}$};

    % arrows
    \path (\myradius*4-3mm, 8mm) edge [line, bend angle=10, bend right]
    node [above, midway] {$h_{11},h_{21}$} (8mm, 8mm);
    \path (8mm, 6mm) edge [line, bend angle=10, bend right]
    (\myradius*4-3mm, 6mm);
    
    \path (\myradius*4-3mm, -8mm) edge [line, bend angle=10, bend left]
    node [below, midway] {$h_{12},h_{22}$} (8mm, -8mm);
    \path (8mm, -6mm) edge [line, bend angle=10, bend left]
    (\myradius*4-3mm, -6mm);

  \end{tikzpicture}
\end{figure}

\begin{alignat*}{3}
  \mathcal{B} \to \mathcal{A}_1:&
  x=h_{11}(u,v)=uv, &\quad&y=h_{21}(u,v)=v \\
  \mathcal{B} \to \mathcal{A}_2:&
  x=h_{12}(u,v)=-uv, &\quad&y=h_{22}(u,v)=-v
\end{alignat*}

\begin{equation*}
  J_1 =
  \left|
  \begin{array}{cc}
    \fpd{uv}{u} & \fpd{uv}{v} \\
    \fpd{v}{u} & \fpd{v}{v}
  \end{array}
  \right|
  =
  \begin{vmatrix}
    v & u \\ 0 & 1 \\
  \end{vmatrix}
  = v,\quad
  J_2 =
  \left|
  \begin{array}{cc}
    \fpd{(-uv)}{u} & \fpd{(-uv)}{v} \\
    \fpd{(-v)}{u} & \fpd{(-v)}{v}
  \end{array}
  \right|
  =
  \begin{vmatrix}
    -v & -u \\ 0 & -1 \\
  \end{vmatrix}
  = v
\end{equation*}

\begin{equation*}
  f_{XY}(x,y) = \frac{1}{\sqrt{2\pi}}\exp\left(-\frac{x^2}{2}\right)
  \cdot
  \frac{1}{\sqrt{2\pi}}\exp\left(-\frac{y^2}{2}\right) =
  \frac{1}{2\pi}\exp\left(-\frac{x^2+y^2}{2}\right)
\end{equation*}

\begin{align*}
  f_{UV}(u,v) &= \sum_{i=0}^2 f_{XY}(h_{1i}(u,v),h_{2i}(u,v))|J_i| \\
  &= \frac{1}{2\pi}\exp\left(-\frac{(uv)^2 + v^2}{2}\right)|v| +
  \frac{1}{2\pi}\exp\left(-\frac{(-uv)^2 + (-v)^2}{2}\right)|v| \\
  &= \frac{v}{\pi}\exp\left(-\frac{v^2(u^2+1)}{2}\right)
\end{align*}

\begin{alignat*}{2}
  f_U(u) &= \int_0^\infty
  \frac{v}{\pi}\exp\left(-\frac{v^2(u^2+1)}{2}\right) dv 
  &\qquad(\text{change of variable: $z=v^2$}) \\
  &= \int_0^\infty \frac{1}{2\pi}
  \exp\left(-\frac{u^2+1}{2}z\right) dz 
  & \left(\int_0^\infty\exp(-\alpha z) dz = 1/\alpha\right) \\ 
  &=\frac{1}{\pi}\cdot\frac{1}{u^2+1}
\end{alignat*}
\end{document}