
\documentclass{beamer}
\usepackage{tikz}
\usepackage{graphicx}
\usetikzlibrary{decorations.text}
\begin{document}
\begin{frame}
\frametitle{Donut and Pictures}
\begin{figure}[h]
\centering
\begin{tikzpicture}
\newcommand*{\myInnerRadius}{1cm}%
\newcommand*{\myOuterRadius}{3cm}%
\newcommand*{\myMidRadius}{2cm}%
% three segments in donut
\filldraw[fill=blue!30, draw=blue!50] (30:\myInnerRadius) -- (30:\myOuterRadius) arc (30:150:\myOuterRadius) -- (150:\myInnerRadius) arc (150:30:\myInnerRadius);
\filldraw[fill=red!30, draw=red!50] (30:\myInnerRadius) -- (30:\myOuterRadius) arc (30:-90:\myOuterRadius) -- (-90:\myInnerRadius) arc (-90:30:\myInnerRadius);
\filldraw[fill=green!30, draw=green!50] (150:\myInnerRadius) -- (150:\myOuterRadius) arc (150:270:\myOuterRadius) -- (270:\myInnerRadius) arc (270:150:\myInnerRadius);
% text around the donut
\path[decoration={text along path, text={Random Text}, text align={align=center}, raise=1ex}, decorate] (150:\myOuterRadius) arc (150:30:\myOuterRadius);
\path[decoration={text along path, text={Another Text}, text align={align=center}, raise=1ex}, decorate] (30:\myOuterRadius) arc (30:-90:\myOuterRadius);
\path[decoration={text along path, text={Last Random Text}, text align={align=center}, raise=1ex}, decorate] (270:\myOuterRadius) arc (270:150:\myOuterRadius);
% image
\node (G1) at (0:0cm) {\includegraphics[height=15mm]{Figs/youtube.png}};
\node (G2) at (90:\myMidRadius) {\includegraphics[height=15mm]{Figs/12.png}};
\node (G3) at (-30:\myMidRadius) {\includegraphics[height=15mm]{Figs/6.png}};
\node (G4) at (210:\myMidRadius) {\includegraphics[height=15mm]{Figs/linkedin.png}};
\end{tikzpicture}
\end{figure}
\end{frame}
\end{document}
#!/usr/bin/env python
class Fibo:
"Class-based Fibonacci recursion"
def __init__(self, n):
if n == 1:
self.value = 1
elif n == 2:
self.value = 1
else:
A = Fibo(n-1)
B = Fibo(n-2)
self.value = A.value + B.value
def __repr__(self):
return str(self.value)
if __name__ == "__main__":
print Fibo(1)
print Fibo(2)
print Fibo(3)
print Fibo(4)
print Fibo(5)
print Fibo(6)
print Fibo(7)
print Fibo(8)
print Fibo(9)
print Fibo(10)
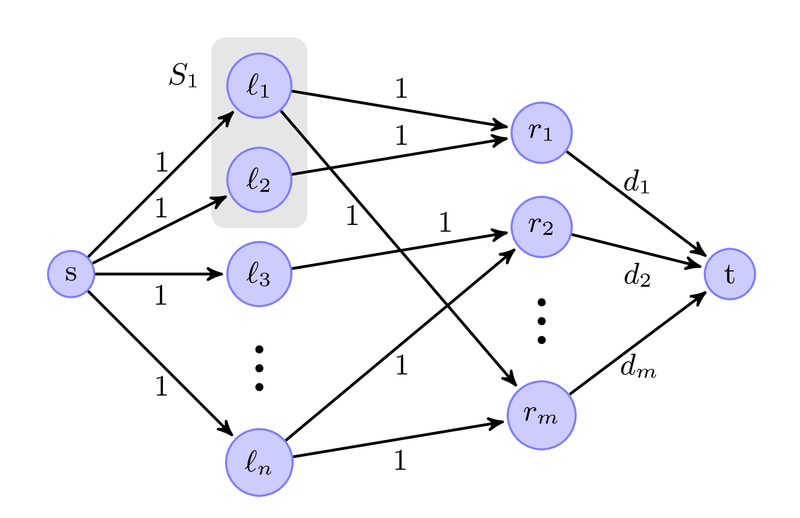
\documentclass[letterpaper,11pt]{article}
\usepackage[papersize={85mm, 55mm}, text={75mm, 45mm}]{geometry}
\pagestyle{empty}
% For automata drawings
\usepackage{tikz}
\usepackage{pgf}
\usetikzlibrary{arrows}
\begin{document}
\begin{figure}[h]
\footnotesize
\centering
\begin{tikzpicture}[
% type of arrow head
>=stealth',
% keep arrow head from touching the surface
shorten >= 1pt,
% automatic node positioning
auto,
%
node distance=2cm,
% line thickness
semithick,
bend angle=10,
graybox/.style = {draw=gray!20, fill=gray!20, rounded corners},
line/.style = {->, draw=black, thick},
box/.style = {circle, draw=blue!50, fill=blue!20, minimum size=4mm}
]
\coordinate (S) at (-5cm, 0cm);
\coordinate (S1) at (-3cm, 2cm);
\coordinate (S2) at (-3cm, 1cm);
\coordinate (S3) at (-3cm, 0cm);
\coordinate (S4) at (-3cm, -2cm);
\coordinate (M1) at (0cm, 1.5cm);
\coordinate (M2) at (0cm, .5cm);
\coordinate (M3) at (0cm,-1.5cm);
\coordinate (T) at (2cm, 0cm);
\node (BBox) [graybox, minimum width=1cm, minimum height=2cm] at (-3cm, 1.5cm) {};
\node [left] at (BBox.130) {$S_1$};
% nodes
\node (Sbox) [box] at (S) {s};
\node (Sbox1) [box] at (S1) {$\ell_1$};
\node (Sbox2) [box] at (S2) {$\ell_2$};
\node (Sbox3) [box] at (S3) {$\ell_3$};
\node (Sbox4) [box] at (S4) {$\ell_n$};
\node (Mbox1) [box] at (M1) {$r_1$};
\node (Mbox2) [box] at (M2) {$r_2$};
\node (Mbox3) [box] at (M3) {$r_m$};
\node (Tbox) [box] at (T) {t};
\fill [black] (-3cm, -.8cm) circle (1.2pt);
\fill [black] (-3cm, -1cm) circle (1.2pt);
\fill [black] (-3cm, -1.2cm) circle (1.2pt);
\fill [black] (0cm, -.3cm) circle (1.2pt);
\fill [black] (0cm, -.5cm) circle (1.2pt);
\fill [black] (0cm, -.7cm) circle (1.2pt);
% edges
\path[line] (Sbox) -- node [above] {1} (Sbox1);
\path[line] (Sbox) -- node [above] {1} (Sbox2);
\path[line] (Sbox) -- node [below] {1} (Sbox3);
\path[line] (Sbox) -- node [below] {1} (Sbox4);
\path[line] (Sbox1) -- node [above] {1} (Mbox1);
\path[line] (Sbox2) -- node [above] {1} (Mbox1);
\path[line] (Sbox3) -- node [above, pos=.7] {1} (Mbox2);
\path[line] (Sbox1) -- node [below, pos=.3] {1} (Mbox3);
\path[line] (Sbox4) -- node [below] {1} (Mbox2);
\path[line] (Sbox4) -- node [below] {1} (Mbox3);
\path[line] (Mbox1) -- node [above] {$d_1$} (Tbox);
\path[line] (Mbox2) -- node [below] {$d_2$} (Tbox);
\path[line] (Mbox3) -- node [below] {$d_m$} (Tbox);
\end{tikzpicture}
\end{figure}
\end{document}
Let G be a d-regular bipartite graph and AG is its adjacency matrix. Prove that the eigenvalue of AG is -d.
One example:
- Let G be a graph where the left vertices are {1,3,5} and the right vertices are {2,4,6}.
- The undirected edges are (1,2), (1,4), (3,4), (3,6), (5,1), (5,6).
octave:1> B=zeros(6,6)
B =
0 0 0 0 0 0
0 0 0 0 0 0
0 0 0 0 0 0
0 0 0 0 0 0
0 0 0 0 0 0
0 0 0 0 0 0
octave:2> B(1,2)=1; B(1,4)=1; B(3,4)=1; B(3,6)=1; B(5,2)=1; B(5,6)=1
B =
0 1 0 1 0 0
0 0 0 0 0 0
0 0 0 1 0 1
0 0 0 0 0 0
0 1 0 0 0 1
0 0 0 0 0 0
octave:3> B = B + B'
B =
0 1 0 1 0 0
1 0 0 0 1 0
0 0 0 1 0 1
1 0 1 0 0 0
0 1 0 0 0 1
0 0 1 0 1 0
octave:4> [EVEC, EVAL] = eig(X)
EVEC =
-0.50000 0.65328 0.50000 -0.27060
-0.50000 0.27060 -0.50000 0.65328
-0.50000 -0.27060 -0.50000 -0.65328
-0.50000 -0.65328 0.50000 0.27060
EVAL =
Diagonal Matrix
1.7413e-16 0 0 0
0 5.8579e-01 0 0
0 0 2.0000e+00 0
0 0 0 3.4142e+00
octave:5>


